





Notes:
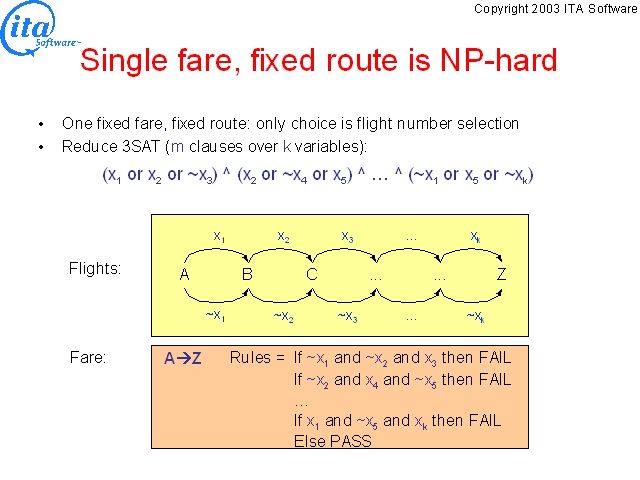
It is possible to reduce the NP-complete 3SAT problem to the question of whether there is a combination of flights that satisfies a particular fare’s rules. For a given 3SAT expression over k variables one can construct a sequence of k+1 airports with exactly two flights between the ith and (i+1)th airport, one flight representing the assignment of true to the ith variable, the other false. It is possible to construct a single fare from the first to the last airport such that the fare’s rules enforce the 3SAT logical expression. This is not entirely trivial to show, in that the limited rule language forces one to apply DeMorgan’s rule to the expression and to encode the restrictions on variables as a certain kind of restriction on the flight numbers that can be used between two specific airports, but the fare rule language is (just barely) expressive enough to do this.
This simple fact is interesting because the airlines often advertise fares to the public: “$100 special from Boston to San Francisco!” Even looking at that fare’s rules, it may not necessarily be easy to find a sequence of flights that will satisfy them.
In point of fact, the particular rule mechanisms used in the complete proof are not usually problematic for search, but the combined set of all types of fare component flight and route and time restrictions can make it very difficult to find valid flight sequences for many fares between airports separated by 3 or more flights (or to prove that no valid sequence exists).












