





Notes:
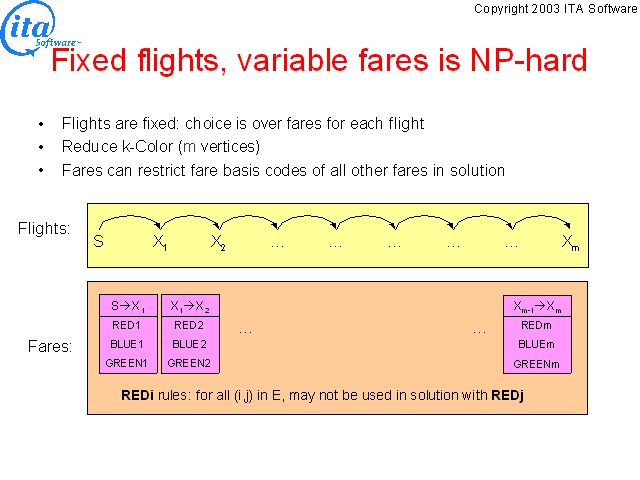
Fixing a sequence of flights but introducing a choice of fares to pay for each flight, it is again possible to reduce an NP-complete problem, k-coloring a graph (coloring graph vertices with k colors such that no two connected vertices share the same color). In this construction vertices are represented by flights and the color of a vertex by the choice of fare used to pay for the flight. A sequence of flights is constructed, one per vertex, and a query posed between the endpoints. The fare database is constructed to contain one fare per combination of vertex and color. In the figure, the fares for the flight representing vertex i are named REDi, BLUEi and GREENi (for 3-color).
It is possible to encode in fare rules restrictions on the fare basis codes of other fares that appear on the same ticket, even if they are in other priceable units. Extra-priceable-unit restrictions on fare combinations are called end-on-end fare combinability restrictions, or end-on-end restrictions. To complete the translation of graph coloring into air travel pricing, if vertex i is connected to vertex j by an edge, then every vertex i fare prohibits the vertex j fare of the same color from appearing on the same ticket. For example, if vertex 3 is connected to vertex 6, then RED3 prohibits RED6, BLUE3 prohibits BLUE6 and GREEN3 prohibits GREEN6.
Again, the only difficulties to this proof consist of finding mechanisms in the airline industry’s rule system sufficiently powerful to encode the original problem. The power of a fare to restrict, even independently, the fare basis codes of all other fares in a solution is simply too powerful for efficient search.
To the extent that one associates NP-hard (NP-complete) problems with exponential time search, this result is extremely important, because in many queries the base and exponent are sufficiently large for exhaustive search to be impossible. For example, for a round-trip query requiring three outbound and three return flights, it may be necessary to search over tickets that use 6 fares per passenger. For each market, there may be 1000 published fares. Finally, if multiple passengers travel there can be interactions between the passengers’ fares. So, for a two person query the search space may be greater than 1000^12, or 10^36. For a completely fixed set of flights!!












